両端固定梁 2点集中荷重 278891

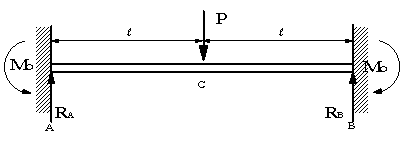
両端固定梁 梁の中間に集中荷重 xbの時 x=aでは x=aでは xaの時 xaの時 ではもし ならば では もし ならば 中心では 中心では 中心では 両端 支持 梁 任意の位置にモーメント付加 の時計算を実行すると、梁のたわみ量(mm)、応力(MPa)、重量(kgf)が出力されます。 Step1 梁の支持方法を選択します。 片持ち 両端支持 両端固定;叱正批判を待つより他ない．お気付きの点をぜひ著者までお寄せ下さい． 最後に，恩師である宇都宮大学工学部機械システム工学科の佐藤啓仁教授に心からの 敬意と謝意を表します．また，同大学院生，大川洋之君，齋藤慶一君，新関亘君，橋 本浩之君をはじめ，その他多くの学部生・院生諸

許容応力度とたわみによる断面算定の考え方 県木連のホームページ 一般社団法人愛知県木材組合連合会

両端固定梁 2点集中荷重

両端固定梁 2点集中荷重-両端固定はりのたわみ計算コマンドです。はりのたわみ計算 オンラインでは複合荷重に対応した梁のたわみ計算をインターネット上から無料でご利用いただけます 設計者のためのポータルサイト CADデータ無料ダウンロード ホーム > 技術計算 > 両端固定はりのたわみ計算 片持ちはり 両端支持 荷重点の間では、仮想断面の左右の外力が変化しないので、せん断力は一定になります。 図のように両端支持梁に3つの集中が銃が作用すると、梁が4区間に分けられて4つのせん断力が発生します。 これらの4つのせん断力f 1 ・f 2 ・f 3 ・f 4 を求めなさい

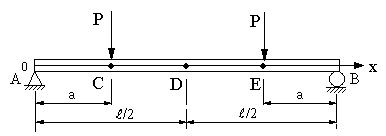
Ex 5

 単純ばりですし、集中荷重は2つありますが、力のつり合いとモーメントのつり合いから簡単に求められます。 鉛直方向の力のつり合いより 5(kN)8(kN)V AV B =0 水平方向の力のつり合いより H A =0 点Bにおけるモーメントのつり合いより V A ・9 (m) – 5(kN)×6(m) – 8(kN)×3(m) = 0 ∴V A =6(kN), H A =0(kN), V B =7両端固定梁の場合 次の 例題は図441の両端固定の 場合であるが，この場合にも例えば図示したような三つの静定系の 重ね合わせで解けそうだ。と が未知の不静定反力である。 等分布外力が作用した梁の 場合には，式()より28 n個の集中荷重 を 411 両端固定 の半円輪 Euler's law）が用いられる．この法則によれば，はりの任意点 における曲げモーメント は，その荷重によって生じる曲率の変化に比例する．たわみ曲線が式s= f(φ) で与えら れるなら，その基礎方程式は 1 r = M EI = dφ ds となる．ここで，sはたわみ

ピン－固定 等分布荷重 ピン 固定梁 ← 図をクリックすると、 各種計算式が表示されます。 反力、せん断、曲げモーメント、 たわみ、・・・ Type 両端固定 中心集中荷重 両端固定 偏芯集中荷重 両端固定 等分布荷重 両端固定 ← 図をクリックすると、 各種計算式が表示されます。 反力L：荷重図 Q：せん力図 M：曲げモーメント図 W：全荷重 M：曲げモーメント R：反力 θ：回転角 Q：せん断力 δ：たわみ 両端固定 中心荷重 両端固定 偏芯荷重 両端固定 等分布荷重 kanpro 公式集－梁 両端固定梁で、ある点2箇所、1点は上から、もう1点は下からの集中荷重がかかる時の撓み計算式御存知の方いらっしゃいましたらご教授下さい。 │___↓_______│ ←この様な感じ │ ↑ │ 締切済み 物理学;

44 例題4集中荷重を受ける両端固定 はり 図1 集中荷重を受ける両端単純支持はり 解 点c で仮想的に分割すると、図2 の下のようになります。 p r1 l r2 1 a b c l2 r1 r2 r1 r2 図2 点c で分割 反力r1 とr2 の和は明らかに r1 r2 = p (1) 式(1) で未知量はr1 とr2。一方、式は一つなので、解けないことになり構造計算資料 梁公式集 1片持梁 2単純梁 3はね出し単純梁 41端ピン他固定 5両端固定梁 6連続梁 7三角形の面積 携帯用壁紙例1：一点集中荷重の両端支持単純梁 まず、この例を通じて、重要な概念である せん断力 と 曲げモーメント について説明したいと思います。 下図のように長さ L の梁をX軸上に置きます。 その両端は支持されていますが回転は許されているとします

単純梁に集中荷重が2箇所にかかっている場合のたわみの算出方法を教えてく Yahoo 知恵袋

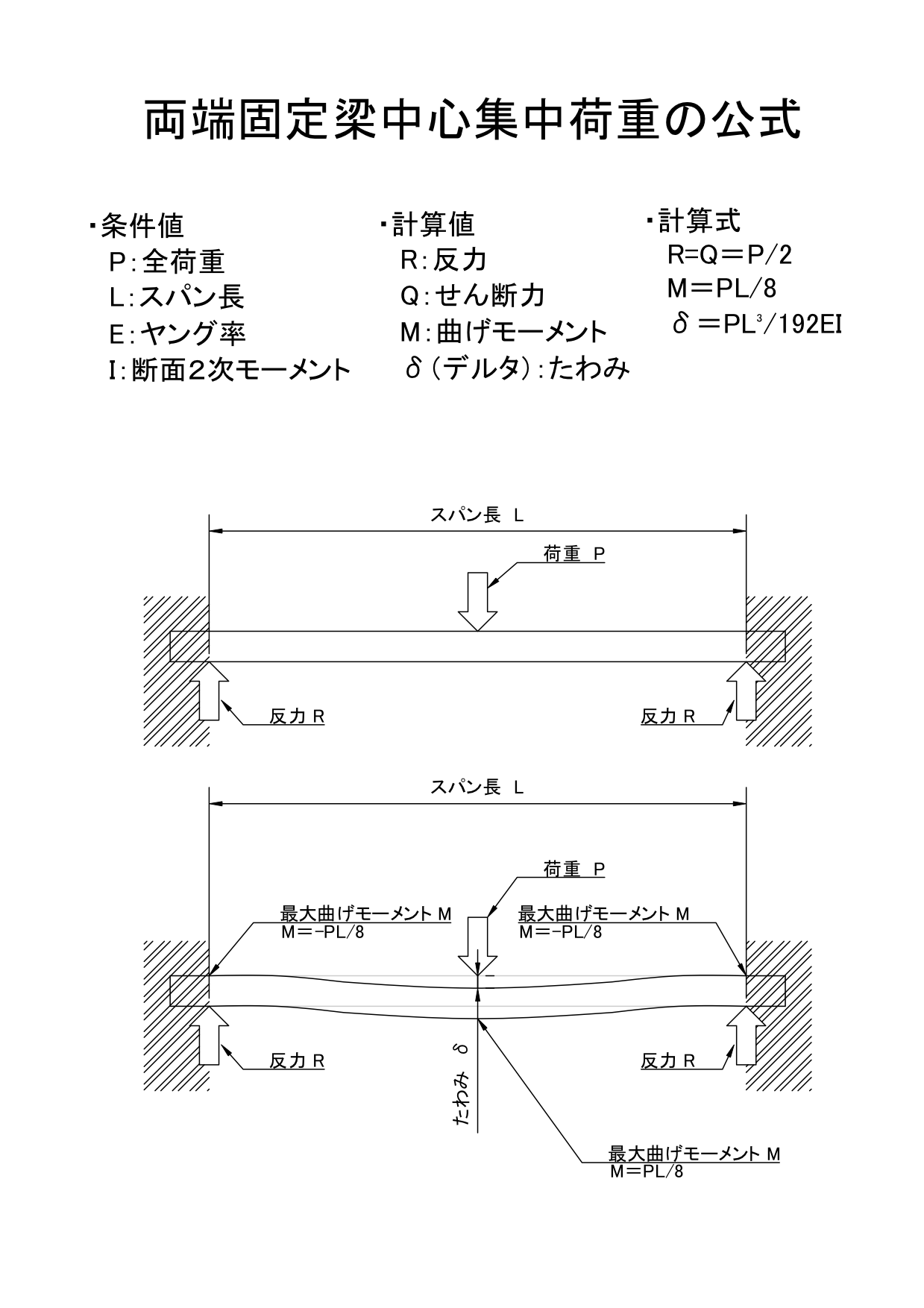
両端固定梁とは 梁の両端を接合 機械卒でも土木の現場監督

結合点Cに水平荷重P=80kNが作用するとき、点Cに生じる水平および鉛直変位δh、δvを求めよ。ただし両棒の横断面積をA=10cm 2 、縦弾性係数Eを21x10 5 MPaとする。 解答例 問題5 図の両端支持はりの場合に、せん断力、曲げモーメント、せん断力図、曲げモーメント図を求める。ただ Q 両端支持梁に集中荷重（2か所）の場合の最大応力 両端支持の梁に2か所の集中荷重が印加された場合の 最大応力σmaxを求める計算方法に関する質問です。 添付図の様に対称位置では公式集にある様な下記の式で求められる事が判りました。 両端固定梁曲げ応力計算例H300、等分布荷重 Next 片持ち梁曲げ応力計算例H300、集中荷重 オフラインのためランキングが表示できません サイト内検索 スポンサーリンク 構造力学 の最新記事8件 片持ち梁せん断応力計算例H300、等分布荷重 片持ち梁曲げ応力計算例H300、等分布

どなたかご教授下さい 2点集中荷重の両端支持はりの指定箇所にかか Yahoo 知恵袋

Excelを使った数値計算ツールsuitexl

 支点A、Bの2か所で支持されている単純両支持の梁に支点Aから距離xの位置に 集中荷重がある時、この梁の最大曲げ荷重のかかる位置はxの位置で良いでしょうか？ 計算方法の正誤を知りたいので、いくらか条件説明は省略させて頂きますが、 まず、支点A,B集中荷重 等分布荷重 片持ち｜集中荷重 Step2 断面を選択します。 ここにない断面は 複合断面のツールで 計算後に 左図任意断面を選択 任意断面 単純梁に集中荷重2つと等分布荷重が作用しているときの最大曲げモーメントの算出方法について教えていただきたく、よろしくお願いいたします。 汚い図で申し訳ありません。 色々と調べたところ重ね合わせの定理を使うと書いてあったのですが、いまいちわからず。。。 お詳しい方、ぜ

両端支持梁の支点反力を求める例題を紹介 建築学科のための材料力学

曲げモーメント せん断力 たわみの計算式 県木連のホームページ 一般社団法人愛知県木材組合連合会

 RA × s1 = RB × s2 ・・・ (2) 式 (1) (2)より、点A、Bに作用する反力R A 、R B がそれぞれ求まります。 以上をまとめると、 集中荷重が作用する梁では、①力のつり合いと②モーメントのつり合いから、支点に作用する反力が求まります。 ちなみに、これは荷重が図632 b点を剛体壁とする2つの片持ちはり 変形後の状態を図633に示す。 図633 変形後の状態 すなわち，集中荷重r1によりa点はa'点に移動しそのたわみ量を 1 ， r2 によりc点はc'点に移動しそのたわみ量を 2とすると，教構造物に作用する荷重モデル 25 • 面積のない点に作用． 集中 • 単位長さあたり等しい強さの力．四角形で表示 等分布 • 単位長さあたりの力が等しい比率で増減する力．三角 形で表示 等変（三角形）分布 • 一点に集中して回転作用が働く 集中モーメント 問題を簡単にするモデル化 26

2点集中荷重片持ち梁について 2点集中荷重片持ち梁の曲げモーメントとたわ Okwave

両端支持のたわみ計算は 1分でわかる計算 公式 両端固定梁のたわみ

C116 講義資料 材料力学 Golden, CO, USA (09) 京都大学農学部地域環境工学科 中嶋 洋 Ver梁の公式 本ソフトは、ユニット化されたアルミ構造材のたわみ量や安全率を計算するソフトウェアです。 片持ち先端荷重 片持ち集中荷重 片持ち等分布荷重 両端支持中心荷重 両端支持任意等分布荷重 両端支持等分布荷重 両端固定中心荷重 両端固定任意等分布荷重 両端固定等分布荷重 両端等分布荷重を受ける単純梁の両端のたわみ角 wl/2 w wl/2 Mx＝wlx/2－wx2/2 x M=1 1/l 1/l Mx＝x/l EI wl l wx wx EI dx l x x w x wl EI MMdx EI l l l A 6 8 24 1)( ) 2 2 (1 1 3 0 3 4 0 2 0 EI wl B 24 3 中間荷重両端モーメント 両端にモーメントが作用 B B A A A B M M EI M M EI 2 6 2 6 等分布荷重と両端にモーメントが同時に作用 EI wl M

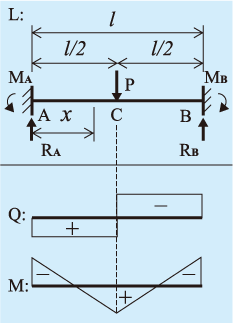
構造計算 両端固定梁 切削 樹脂 プレス レーザー加工の特急試作なら日新産業株式会社

2点集中荷重が作用する両端固定梁の公式は 1分でわかる求め方 解き方 と計算

 集中荷重（片持ち梁は先端荷重）の場合 $$\theta = \frac{PL^2}{ EI}$$ 等分布荷重の場合 $$\theta = \frac{wL^3}{〇〇EI}$$ この傾向をつかんだだけでも、少しは覚えるハードルが下がった気がしませんか？Q&A一覧 公式・専門家 質問・相談 「両端固定梁」の検索結果 質問一覧 画像の等分布荷重を受ける両端固定梁のA点及びB点に生じるモーメントの求め方を教えて欲しいです。 答え 答えは Ma = wol^2/12 Mb = wol^2/12 になるそうです。 分かる方よろしくお願い 412 単純梁の集中荷重 の あと、両端固定（固定梁）のたわみだけ覚えましょう。 固定梁（不静定構造物）の集中荷重と等分布荷重のたわみだけ覚えちゃいまょう！。 上の表と見比べながら読んでいくといいかな♪。 いつなる流の両端固定のたわみの覚え方 どちらも分母をさんばし

Ex 5

両端支持梁に集中荷重 2か所 の場合の最大応力 両端支持の梁に2か所 物理学 教えて Goo

下図に示す部材中央に集中荷重が加わる両端固定梁を解析モ デルとし、部材の変形状態、載荷点の鉛直変位、曲げモーメント分布な どを求める。 x 図111 両端固定梁の解析モデル 変位と荷重には以下のような関係がある。 4 4 zw() dw EI P x dx = ここで、Pw()x は分布荷重であり、x の関数で ある長さ400mmの単純支持はりの中央に集中荷重Pが作用する。はりは、図のようなH型鋼で、許容曲げ応力が 80MPaのとき、安全な荷重の大きさを求める。ただし、b=50mm,h=60mmm,t 1 =10mm,t 2 =mmである。 解答例 問題162 図の梁の場合、たわみ曲線とB,Cにおける曲げモーメントを求める。 解答例両端支持のたわみ計算は、荷重条件と支持条件で変わります。集中荷重が作用する単純梁のたわみ＝pl 3 /48eiです。 等分布荷重が作用する単純梁のたわみ＝5wl 4 /384eiで求めます。 今回は両端支持のたわみ計算、公式、両端固定梁のたわみについて説明します。

たわみ計算 2点集中荷重 両端支持梁 A 物理学 教えて Goo

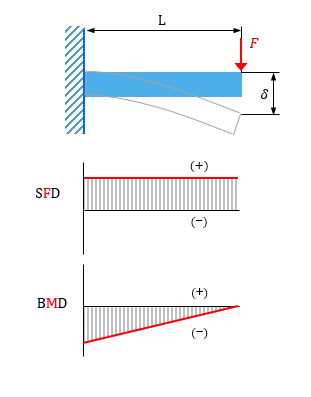
梁のたわみと応力計算ツール

 片持はりに集中荷重が作用する場合のたわみの公式 長さsの片持はりの自由端に、集中荷重Pが作用する場合のたわみの公式は、以下のとおり。 固定端Aでたわみは0、自由端Bでたわみは最大となります。 y(x) = P(x 3 – 3xs 2 x 2s 3)/6EI y max = Ps 3 /3EI梁の公式 荷重・形状 条件 曲げモーメント m反力 r･せん断力 q･全荷重 w たわみ δ P l ab c Ra Rb 2 ra＝rb＝ w＝p p 2 p mc＝ δc＝ 48ei pl3 P l c Ra Rb ab w＝p ra＝qa＝ pb rb＝－qb＝ pa mc＝ δc＝ pab 3eil 2 2 P l c Ra Rb P c l/3 l/3 l/3 ra＝rb＝p qa＝－qb＝p w＝2p 3 pl ＝mmax δmax＝ 648ei 23pl3 3 δc＝ 162ei 5pl P l Ra Rb P P c l/4 l/4 l/4 l片持ばり以外の例では，中央に集中荷重を受ける両端支持はりではα=48であり，両端固定はりではα=192となります． では次の問題に取り組んでみましょう． 問題54 図514に示す長さl=300mmの軸の中央にP=300Nの集中荷重がかかっています．許容できるたわみ量δを001mmとして，両端支持および

Ex 5

梁の計算7 両端固定梁 等分布荷重 Youtube

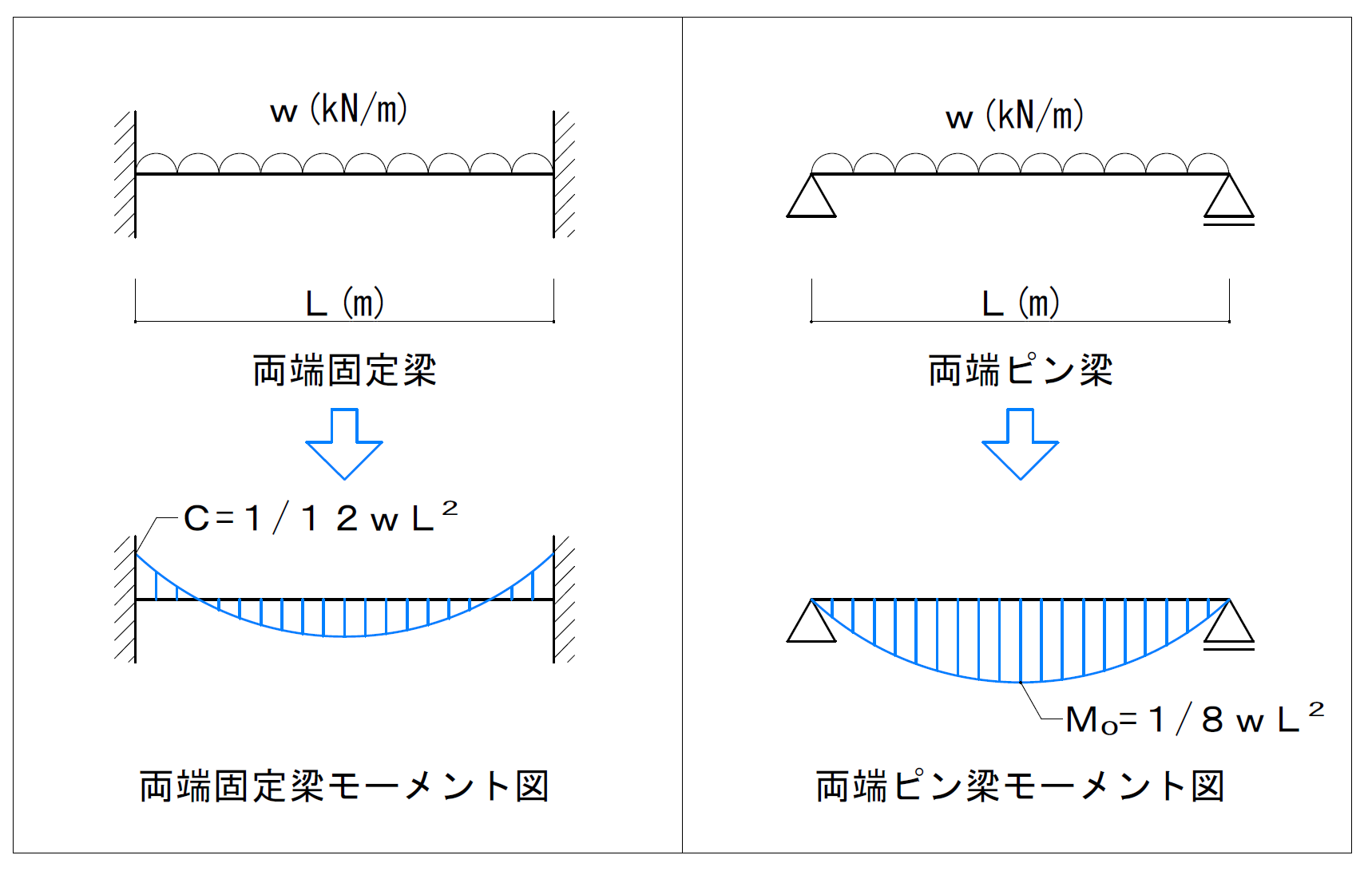
単純梁と両端固定梁を比較単純梁の方が変位が大きい 最大せん断力については集中荷重・等分布荷重どちらも同じである。 荷重を負担するのが両端2箇所で同じであるため、同様の値となる。 最大曲げモーメントはどちらの荷重条件でも単純梁のほう自由端：固定されていない端 ・両端支持はり 両端で自由に回転できる ように支持されたはり 単純支持はりともいう (2) はりに作用する荷重 ・集中荷重 1点に集中して作用する荷重 ・分布荷重 はりの全長、または一部分 に分布して作用する荷重 ・等分布荷重 単位長さあたりの荷重が なので、両端固定梁の中央部曲げモーメントは『1/8wL 2 －1/12wL 2 =1/24wL 2 』と公式を暗記せずとも求められます。 この端部が固定されてモーメント図がグググッと持ち上がる感覚、設計者として大事なのかなぁという気がします 集中荷重の場合 梁の中央に集中荷重が作用している

Wo18 号 梁接合構造 梁接合構造の設計方法 及び梁接合構造の製造方法 Astamuse

単純梁の計算公式 対称２点集中荷重

直荷重Pが作用した場合、A、C点の鉛直反力の絶対値として、正 しいものは次のうちどれか。ただし、梁は等質等断面とする。（H5） 2l0 2 40l p a c b 過去問56 同じ単純梁が等分布荷重wおよび集中荷重Pを受け る場合の梁の中央の鉛直変位が ei wl a 384 5 4 g基本的な両端固定梁の等分布荷重と集中荷重のモーメントを求める公式は次のようになります。 等分布荷重時 両端M＝(1/12)wl 2 中央M＝(1/24)wl 2 M：モーメント(kN・m) w：等分布荷重(kN/m) l：スパン(m) それぞれ単位に注意しましょう。 集中荷重時 よって、（2）は×。 （3）集荷中の作用する片持ち梁 続いて、（3）では片方が固定端の片持ち梁に集中荷重がかかっています。 固定端はピン支点やローラー支点と違い、曲げモーメントも生じます。そのため、この部材の左側は固定され、図の点線のよう

電卓で構造計算 スラブ編

モールの定理 集中荷重編 たわみの公式を忘れても求められる とある若手構造設計者の徒然blog

図に示すような２つの集中荷重 P1 600n P2 10nをうけるハリの半 Yahoo 知恵袋

4 3 重ね合わせの原理で不静定梁を解く

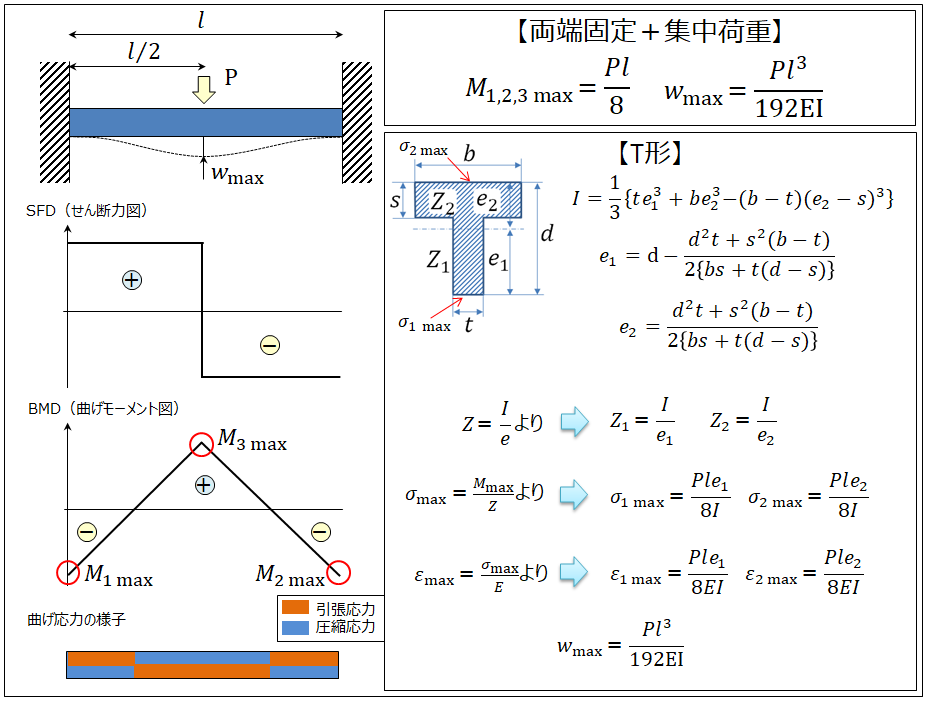
はりの強度計算 両端固定ー集中荷重ーt形 製品設計知識

はりの曲げモーメントせん断力解説

わかりやすい 詳細 等分布荷重を受ける単純支持はりのたわみ

Excelを使った数値計算ツールsuitexl

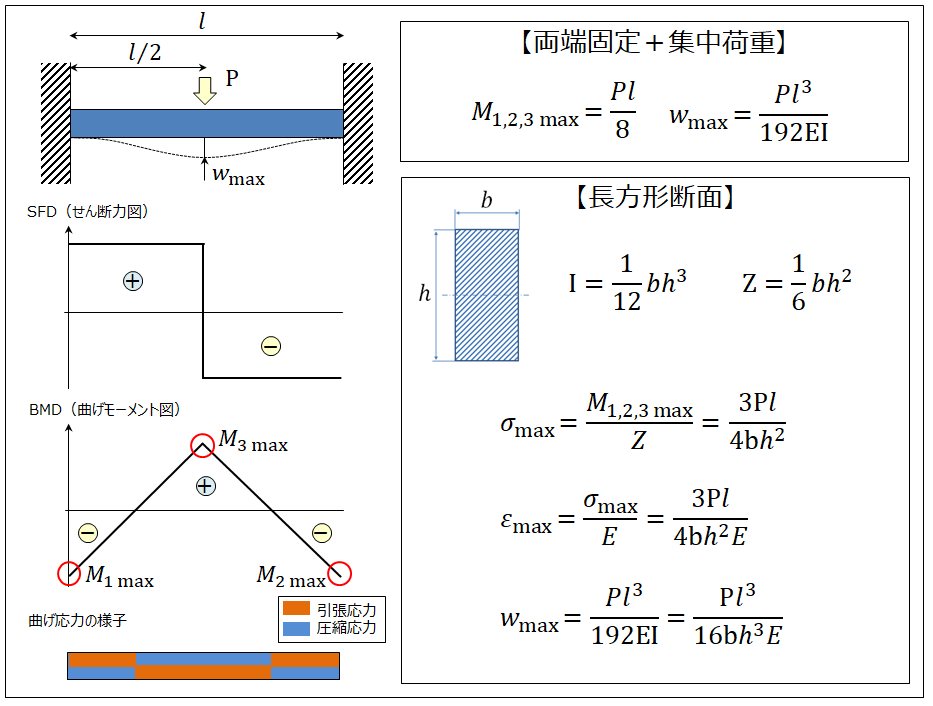
はりの強度計算 両端固定 集中荷重 長方形 製品設計知識

第８章 構造解析法への適用

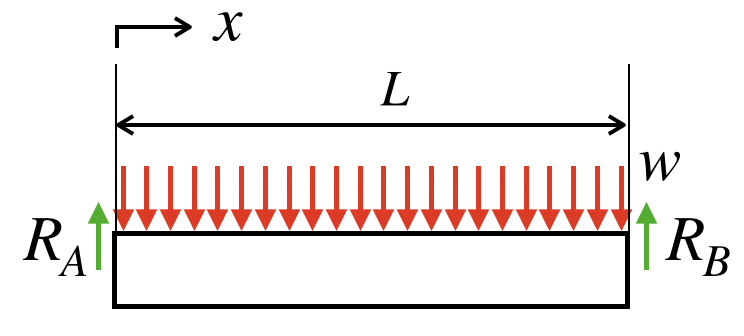
計算を簡略化 等分布荷重のsfd Bmdの書き方 ものづくりのススメ

第８章 構造解析法への適用

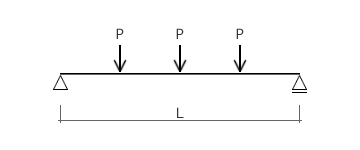
Dansan 公式

4 1 梁の境界値問題

2点集中荷重が作用する両端固定梁の公式は 1分でわかる求め方 解き方 と計算

梁の計算5 両端固定梁 集中荷重 2 Youtube

01 2813号 荷重支持構造 Astamuse

やさしい実践 機械設計講座

材料力学 梁のたわみに関しての質問です 両端固定梁 2点集中荷重はりの最大た Yahoo 知恵袋

両端支持梁に集中荷重 2か所 の場合の最大応力 Okwave

両端固定はりのたわみ計算 はりのたわみ計算 オンライン

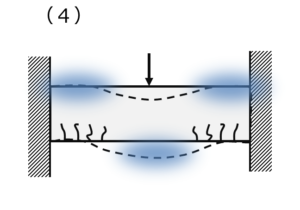
コンクリート技士 主任技士 どこにひび割れが入る コンクリート構造に関する問題

4 3 重ね合わせの原理で不静定梁を解く

種々のはりのたわみ

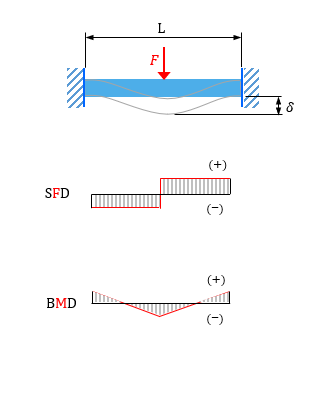
梁のたわみと応力計算ツール

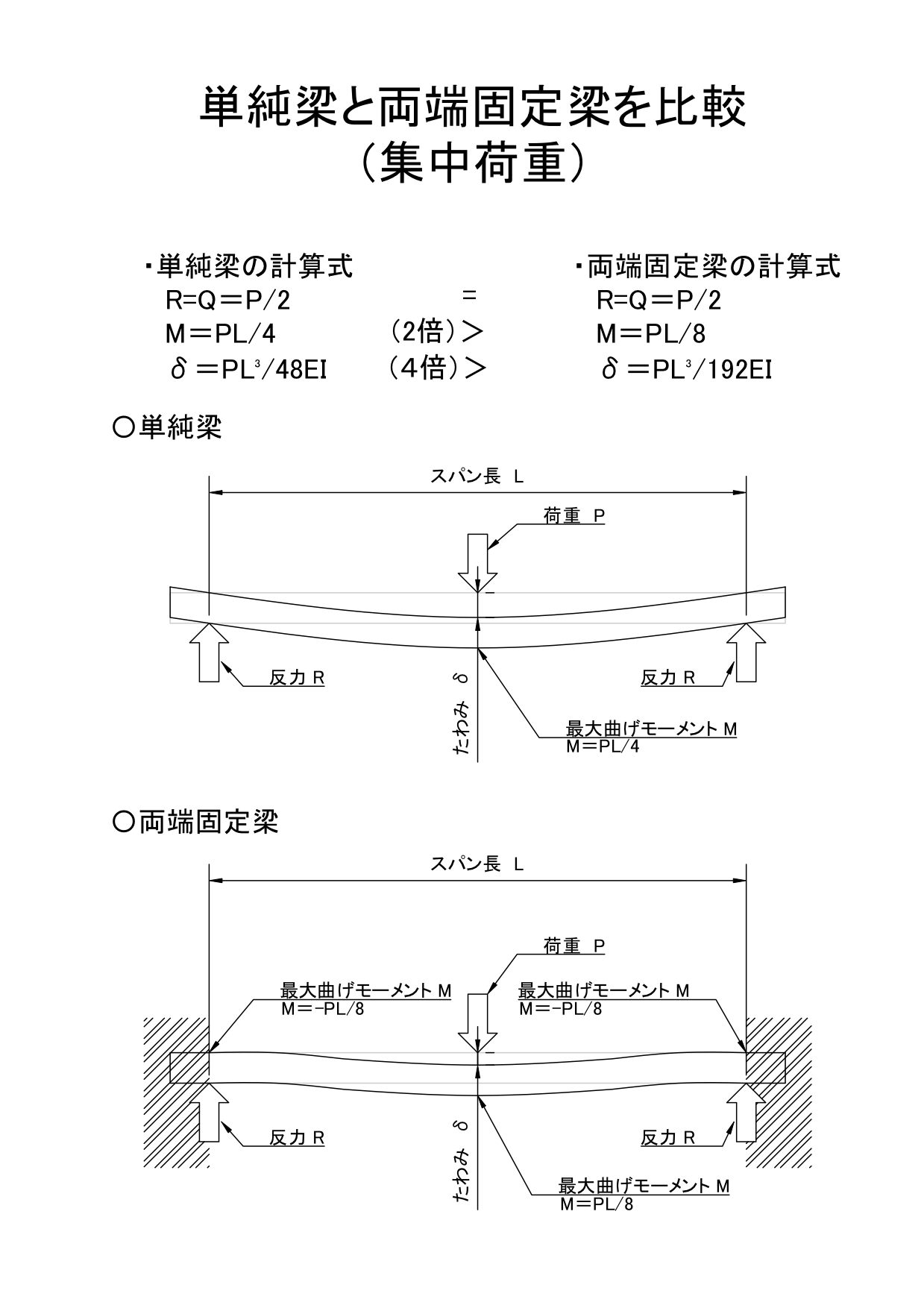
単純梁と両端固定梁を比較 単純梁の方が変位が大きい 機械卒でも土木の現場監督

はりの話 前編

コンクリート技士 主任技士 どこにひび割れが入る コンクリート構造に関する問題

02 はりの曲げ 集中荷重が作用するとき 材料力学の事前 事後学習課題作成のヒント

公式集 構造計算 両端固定梁 曲げモーメント せん断 反力 たわみ

梁 反力 曲げモーメント たわみ 曲げ応力 公式集 計算ツール ものづくりのススメ

Www Jp Omega Com Techref Pressure43 67 Pdf

許容応力度とたわみによる断面算定の考え方 県木連のホームページ 一般社団法人愛知県木材組合連合会

両端支持梁の曲げモーメントの求め方は 計算方法について 建築学科のための材料力学

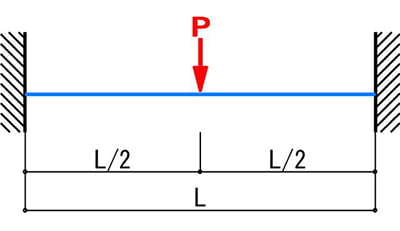
棚板の耐荷重の考え方と 耐荷重計算のやり方を解説します とある建築士の憂鬱

やさしい実践 機械設計講座

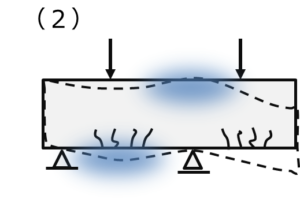
コンクリート技士 主任技士 どこにひび割れが入る コンクリート構造に関する問題

両端固定梁のたわみ 応力 支持反力 集中荷重

両端固定はりのせん断力と曲げモーメント 図のような固定はりのせん断 工学 教えて Goo

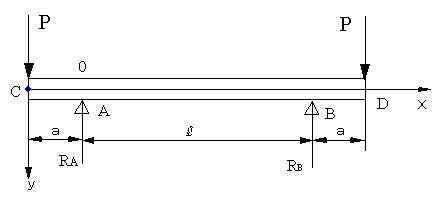
Ex 3

公式集 構造計算 両端固定梁 曲げモーメント せん断 反力 たわみ

第８章 構造解析法への適用

わかりやすい 詳細 三角形状分布荷重を受ける単純支持はりのたわみ

4 在来船の甲板強度 Deck Strength

はりの曲げモーメントせん断力解説

せん断力図の書き方について 両端支持梁に集中荷重が作用した時はどうなる 建築学科のための材料力学

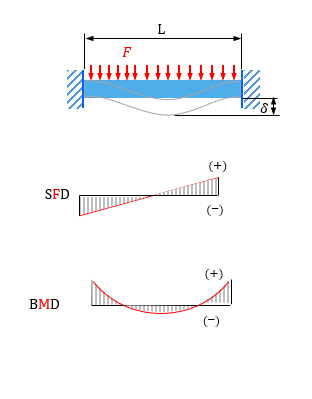
梁のたわみと応力計算ツール

許容応力度とたわみによる断面算定の考え方 県木連のホームページ 一般社団法人愛知県木材組合連合会

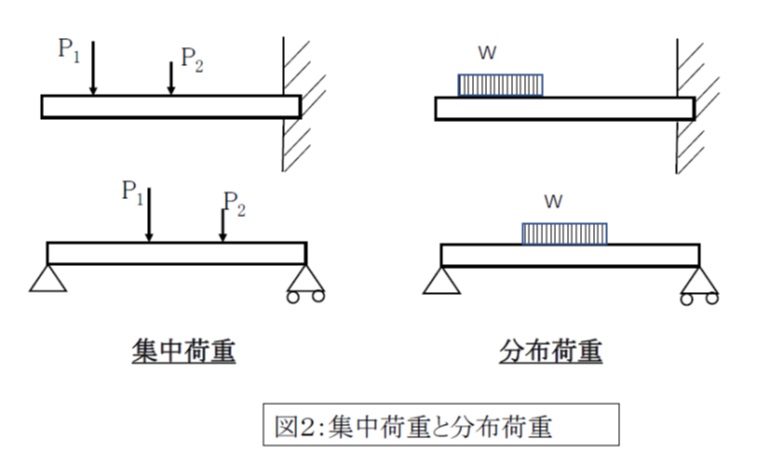
機械設計マスターへの道 はり の基礎知識を習得 Sfdとbmd たわみの計算方法は アイアール技術者教育研究所 製造業エンジニア 研究開発者のための研修 教育ソリューション

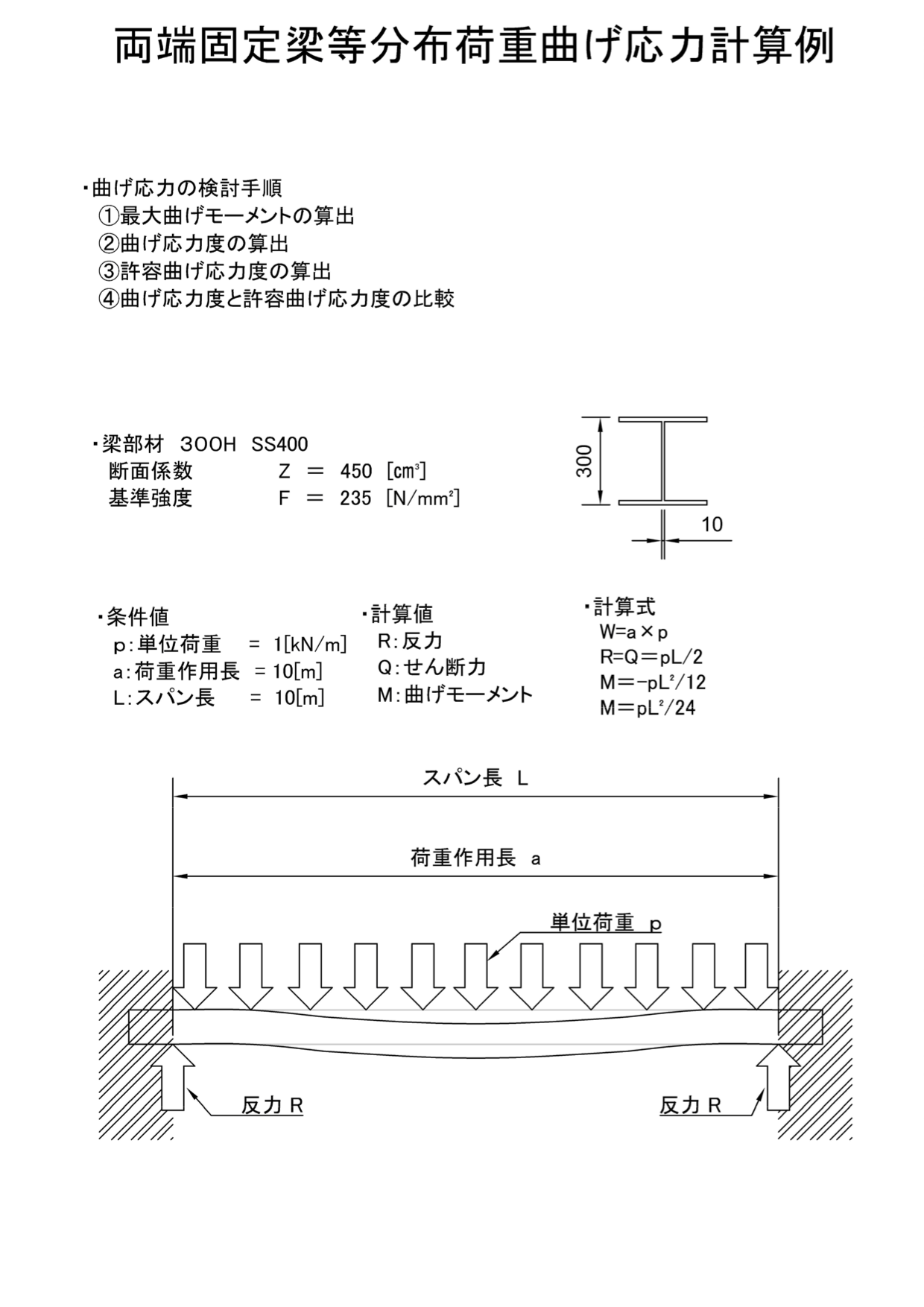
両端固定梁曲げ応力計算例 H300 等分布荷重 機械卒でも土木の現場監督

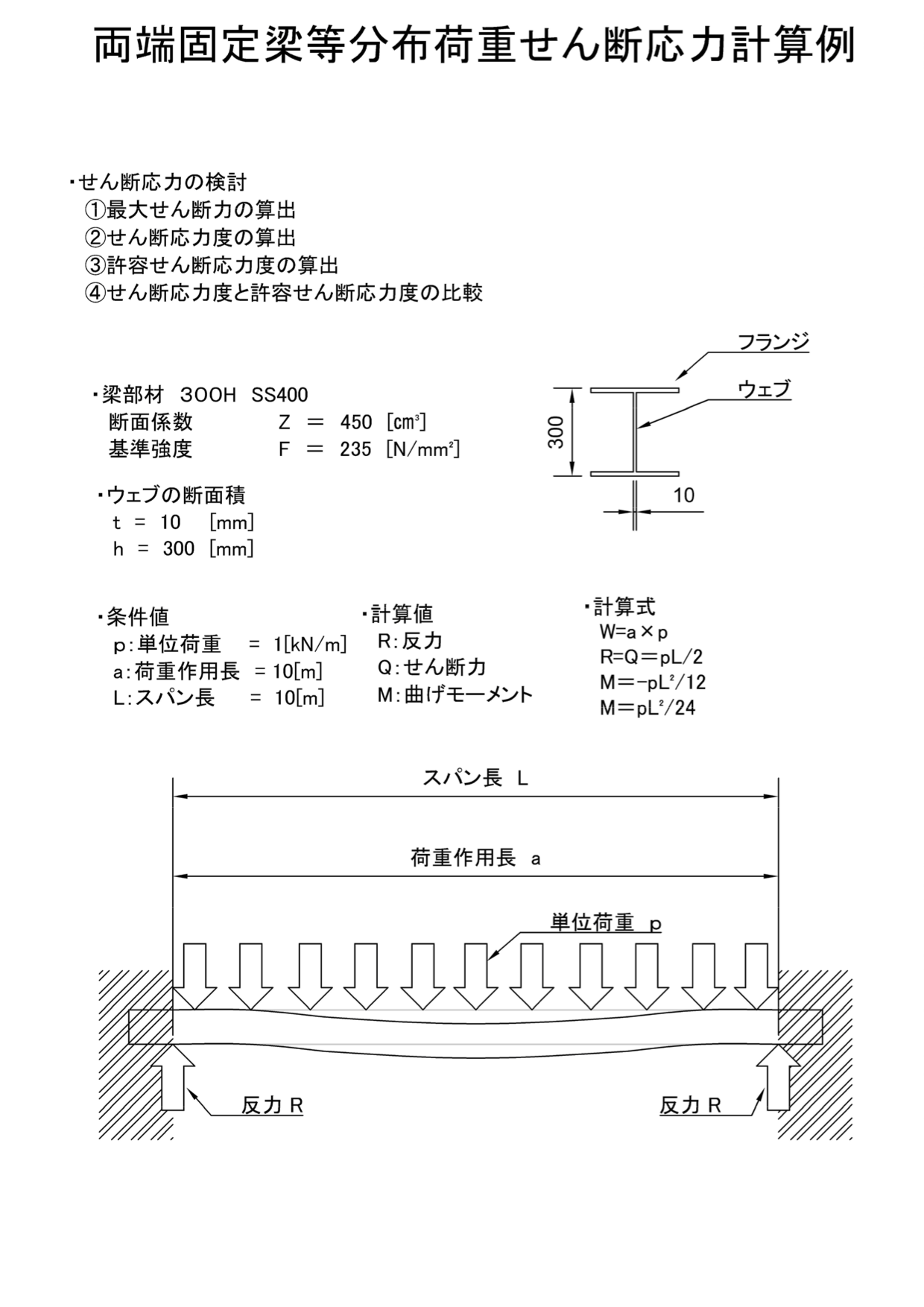
両端固定梁せん断応力計算例 H300 等分布荷重 機械卒でも土木の現場監督

両端支持梁のせん断力計算問題 複数の集中荷重を受ける場合 建築学科のための材料力学

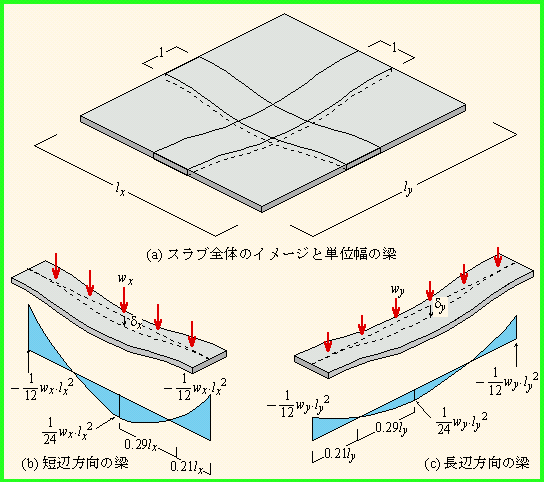
8 2 周辺固定スラブ

片持ち梁に2個の集中荷重が作用するとき 添付図のような片持ち梁があります Okwave

両端固定の梁に任意の位置に集中荷重がかかる場合の 任意の位置のたわみの公式が Yahoo 知恵袋

はりの話 前編

小梁の設計 C M Qとは 構造設計memo

材料力学の問題です 両端固定ばりabが図6 15に示すように一部分に一様 Yahoo 知恵袋

曲げモーメントの公式は 1分でわかる公式 導出 両端固定 単純梁 片持ち梁

2点集中荷重が作用する両端固定梁の公式は 1分でわかる求め方 解き方 と計算

2点集中荷重が作用する両端固定梁の公式は 1分でわかる求め方 解き方 と計算

２点集中荷重の計算について教えてください Okwave

久々の構造力学 一級建築士memo

片持ちばり のsfdとbmd 集中荷重と等分布 三角分布荷重の3パターンの計算を解説するよ のぼゆエンジニアリング

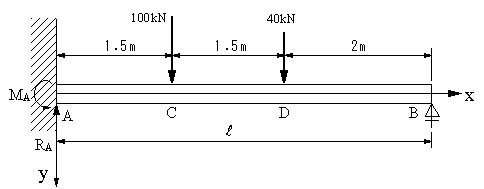
Ex 4

集中荷重が掛かる片持ちハリの曲がる形は ｆ 物理学 教えて Goo

やさしい実践 機械設計講座

曲げモーメント せん断力 たわみの計算式 県木連のホームページ 一般社団法人愛知県木材組合連合会

両端支持のたわみ計算は 1分でわかる計算 公式 両端固定梁のたわみ

たわみ計算 2点集中荷重 両端支持梁 A Okwave

曲げモーメントの公式は 1分でわかる公式 導出 両端固定 単純梁 片持ち梁

21年度2級建築施工管理技士 問題と解説

2点集中荷重片持ち梁について 2点集中荷重片持ち梁の曲げモーメントと 数学 教えて Goo

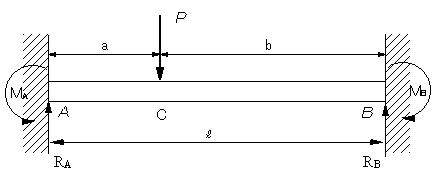
Ex 5

両端固定で集中荷重が2点 両端からa離れ の時の曲げモーメン Yahoo 知恵袋

Stage Tksc Jaxa Jp Taurus Member Miyazaki Old Lecture Strength Of Materials Ii 15 Pdf

Be3

コンサルhiroの構造解析入門講座 梁の公式2 曲げモーメントによる梁内の応力と梁のたわみ

曲げモーメント せん断力 たわみの計算式 県木連のホームページ 一般社団法人愛知県木材組合連合会

両端支持はりの計算 はりのたわみ計算 オンライン

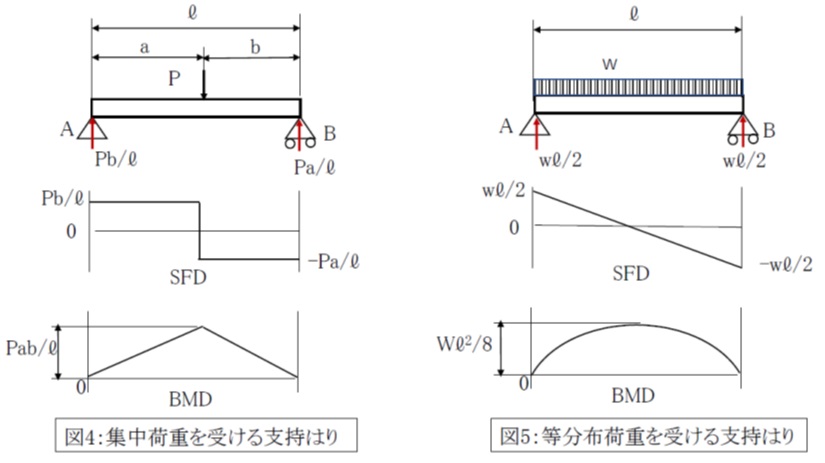
機械設計マスターへの道 はり の基礎知識を習得 Sfdとbmd たわみの計算方法は アイアール技術者教育研究所 製造業エンジニア 研究開発者のための研修 教育ソリューション

単純梁の曲げモーメント 計算 分布 関係